Sometimes, an AI will need to search for a solution in scenarios where one or multiple opposing agents are actively working against it. A prime example of this dynamic is evident in games, where one tries to make intelligent moves while an opponent makes moves in the opposite direction. Such search problems are commonly referred to as adversarial search.

I want to gain a better understanding of how AI actually works. As a first step, I’ve enrolled in the HarvardX: CS50’s Introduction to Artificial Intelligence with Python course on EdX. To enhance my learning, I will be applying the techniques of Nobel Prize winner Richard Feynman and try to teach the concepts I’m learning while I’m learning them. That is what these blog posts will be about. You can find the whole CS50 AI-course straight from FreeCodeCamp’s Youtube channel or on EdX.
Table of contents
Open Table of contents
Introduction
A fairly well-known algorithm used in adversarial search is the Minimax algorithm. In this post, we will dive into the ins and outs of how this algorithm works. We will be using the classic Tic Tac Toe game as an example.
Before we begin, I’d like to mention that I’ve actually previously attempted this algorithm some years back while working on The Odin Project. By the end of this article, I’ll share a link to my unbeatable Tic Tac Toe game, which was the result of those efforts.
Tic Tac Toe
In Tic Tac Toe, one player places an X, then the other player places an O until one player obtains three in a row or there is a draw. Every move should be played to block the opponent or somehow gain an advantage. And with every move, there’s a new state to react to. Minimax is a highly effective algorithm for such scenarios, where each agent takes turns making moves in an attempt to secure victory and force the opponent to lose.
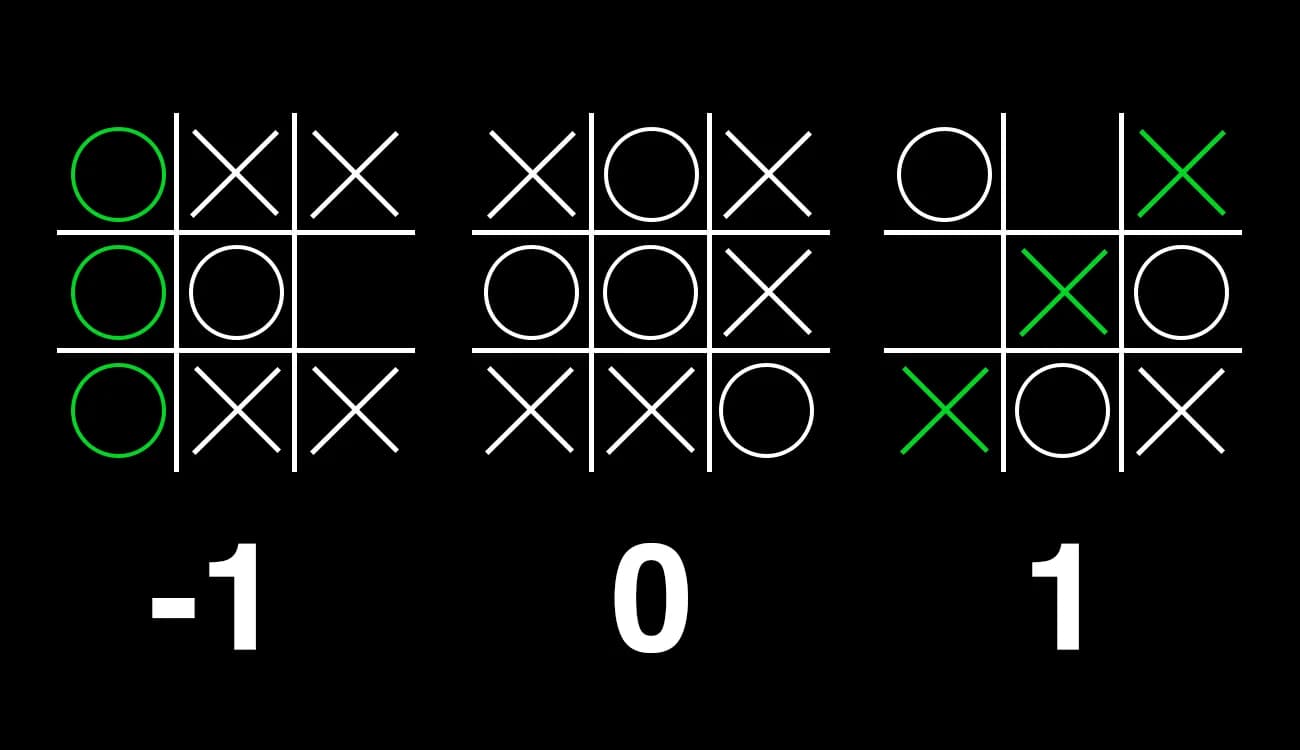
To enable the computer to comprehend winning and losing in a game, we must translate these scenarios into something it can process. Computers operate on numbers. In a game of Tic Tac Toe, there are three possible outcomes: X wins, O wins, or a draw. Each of these situations can be assigned a score in the following way:
Components
Now, each agent has a goal to reach. The X player, or MAX player, will try to maximize its score, while the O player, or MIN player, will try to minimize it. Taking the MAX player as an example, this means that they will attempt to make a move that leads to a score of one. If this isn’t possible, they will strive to make a move that results in a draw, always selecting the option that leads to the maximum available score. The same principle applies in the opposite direction for the MIN player.
Now, let’s examine the components needed to encode this in a way that an AI can play the game. We will require the following elements:
| Component | Description |
|---|---|
| S0 | Initial state |
| Player(s) | Returns which player will move in state s |
| Actions(s) | Return legal moves in state s |
| Result(s, a) | Returns state after action a is taken in state s |
| Terminal(s) | Checks if state s is a terminal state |
| Utility(s) | Final numerical value for terminal state s |
In the case of Tic Tac Toe, the initial state is simply an empty game board. We could represent this by using a two-dimensional array:
[[EMPTY, EMPTY, EMPTY],
[EMPTY, EMPTY, EMPTY],
[EMPTY, EMPTY, EMPTY]]If we feed this to the Player function, we get X in return because X always moves first.
Player(
[[EMPTY, EMPTY, EMPTY],
[EMPTY, EMPTY, EMPTY],
[EMPTY, EMPTY, EMPTY]]
) = XIf X had already made a move, we would have gotten O in return.
Player(
[[EMPTY, EMPTY, EMPTY],
[EMPTY, X, EMPTY],
[EMPTY, EMPTY, EMPTY]]
) = OThe actions function takes a state and returns a set of possible actions, like this:
Actions(
[[EMPTY, X, O],
[O, X, X],
[X, EMPTY, O]]
) = {(0, 0), (2, 1)}The above function returns a set with two tuples, (0, 0) and (2, 1). The example uses indexes starting from 0. The way to read this is the first row and the first column is a possible move, and the third row and the second column is a possible move. Alternatively, a more visual representation:
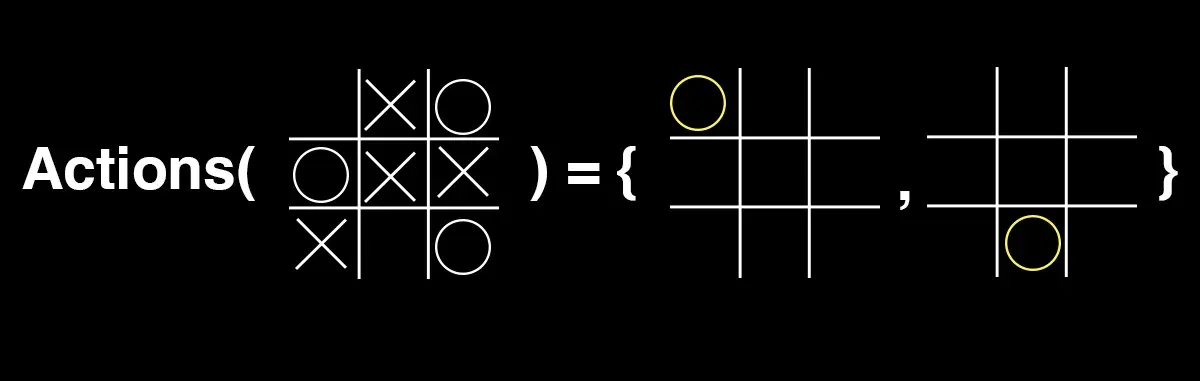
The Result function takes a state and an action and returns the resulting state. O places its marker in the upper left corner:
Result(
[[EMPTY, X, O],
[O, X, X],
[X, EMPTY, O]],
(0,0)) = [[O, X, O],
[O, X, X],
[X, EMPTY, O]]This is, of course, obvious to humans who have played Tic Tac Toe, but for a computer to understand it, we need to code these functions. Similarly, we need to code the function Terminal that informs the AI when we have a state that ends the game: when there are three in a row vertically, horizontally, or diagonally, or when there are no more available moves and the game ends in a draw.
Finally, we have the Utility function that returns the value of the terminal state. As we previously defined: a terminal state where X wins has a value of 1, a draw has a value of 0, and a state where O wins has a value of -1.
The Minimax algorithm
We now have all the pieces we need. The role of the minimax algorithm is to calculate a value for each move that an agent can make at a given state. It will do this by going through all the resulting states that will result from each move and the following states, based on the assumption that X will try to maximize the value of each move and O will try to minimize the value of each move. Sounds a bit complicated, but it will make more sense when we illustrate it.
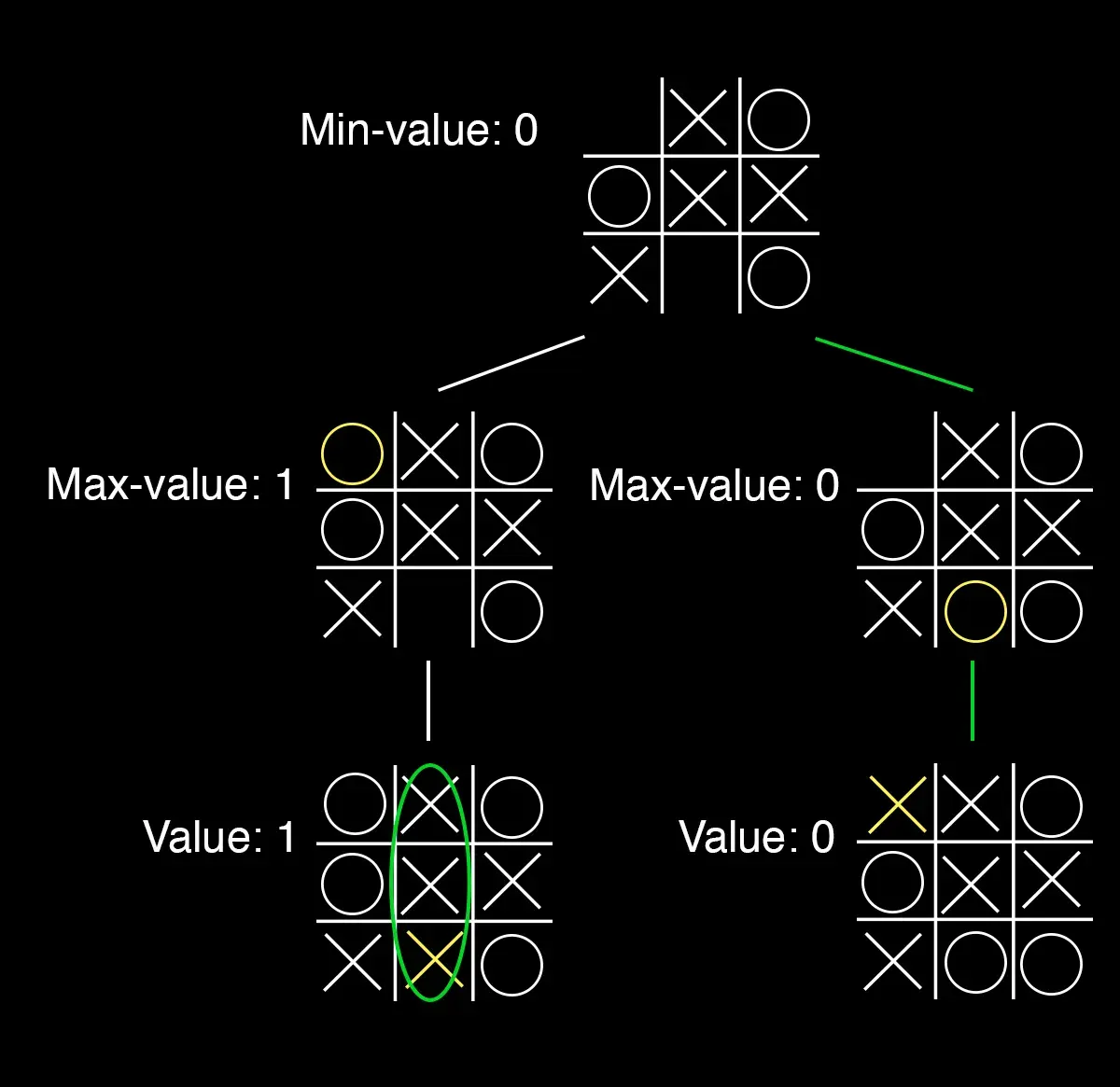
In the situation above, O has two choices. Let’s first explore the left path. Placing the O in the upper left corner creates a state where X only has one move: placing an X in the middle of the bottom row. X will always try to maximize its moves, but here it only has one choice. The utility value of the terminal state resulting from the move X makes is one because we get three Xs in a row. This means the minimum available value O moving down this path will be 1. Similarly, if we explore the right path, it will ultimately end up in a draw with a minimum value of 0. As O always makes moves that minimize the value, it will choose the right path leading to a draw. In other words, the minimum available value of the starting board in our example is 0.
If we are close to the beginning of the game, this tree will, of course, become much deeper. To simplify this a bit, we’ll illustrate the different game states with triangles. A green triangle pointing up is a maximizing state, and a red triangle pointing down is a minimizing state. We will also move beyond utility scores in the range of -1 and 1.
Let’s formalize this process with some pseudocode. This is the premise we want to formalize: Given a state s: MAX picks action a in Actions(s) that produces highest value of MIN-value(Result(s, a)) MIN picks action a in Actions(s) that produces lowest value of MAX-value(Result(s, a))
With pseudocode it could like something like this:
function MAX-value(state):
if Terminal(state):
return Utility(state)
v = -infinity
for action in Actions(state):
v = MAX(v, MIN-value(Result(state, action)))
return v
function MIN-value(state):
if Terminal(state):
return Utility(state)
v = infinity
for action in Actions(state):
v = MIN(v, MAX-value(Result(state, action)))
return vMinimax is a recursive function. A recursive function is one that calls itself. We can observe this as the MAX-value and MIN-value functions call each other repeatedly until a terminal state is reached and we obtain a value for a state.
How to optimize Minimax
Going through all the different possibilities is not a very efficient approach. There are some ways we can optimize the Minimax algorithm.
One way to optimize Minimax is through Alpha-Beta pruning. This involves halting the consideration of possibilities if we can already determine that we can’t achieve a better result. A maximizing agent might encounter a result that is lower than a previous option and then no longer needs to continue examining that branch of the tree. This approach allows us to expand fewer nodes.
When attempting to play a more complex game, we may encounter another problem: there might be too many different solutions for us to explore exhaustively. In such situations, we can employ an approach called Depth-Limited Minimax. This method involves deciding to explore only a certain number of levels down the game tree, such as ten or twenty levels, before halting. However, we then face the challenge of determining the value of the state at that depth.
To address this, we will incorporate an additional function into Minimax. We require an evaluation function that estimates the expected utility of the game from a given state. The efficacy of this evaluation function determines the proficiency of our AI. The more accurately the function estimates the value of a state, the more adept our AI becomes at playing the game.
Play my impossible Tic Tac Toe game
As promised at the outset of this text, I will share my own attempts at implementing the Minimax algorithm. I wrote this code back in 2021 and haven’t revisited it since, but I’m fairly certain it doesn’t precisely adhere to the structure described in the pseudo code we created earlier. Nonetheless, it should adhere to the principles of Minimax. You can review the code on my Github profile. Additionally, you can play the game here.